Scelta dei nodi: entropia e guadagno di informazione
Consideriamo un problema di classificazione (come quello precedente) con le sole due classi “+” (Rischio Alto) e “-” (Rischio Basso), e sia S l’insieme di record (training set) mediante i quali vogliamo costruire un albero di decisione.
Se indichiamo con P+ la percentuale di record classificati con + e con P- la percentuale di record classificati con -, si definisce entropia di S (training set), l’espressione: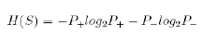
H(S) assume valori compresi tra 0 e 1. E’ pari a 0 quando la totalità dei record è classificata in una sola classe, a 1 quando i record sono equiripartiti tra le due classi.
Andamento dell’entropia nel caso di due classi P+ e P-
Dobbiamo assumere che il log0 = 0.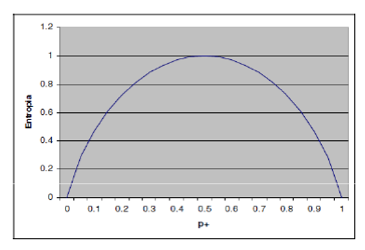
ENTROPIA = 1 : massimo disordine informativo, perché metà osservazioni stanno in un classe e metà nell’altra. Se mi arriva una nuova informazione ho un rischio del 50% di metterla nella classe giusta.
ENTROPIA = 0 : l’osservazione o sta da una parte o sta dall’altra.
Devo scegliere l’attributo in modo tale che mi permetta di ottenere sottoinsiemi in cui l’entropia è vicina allo 0.
Più in generale, se i record del training set sono classificati in c classi, l’entropia si definisce come: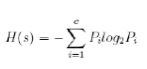
L’entropia è una misura del disordine (o dell’ordine) del training set utilizzato per la costruzione dell’albero. Un valore elevato di entropia esprime un elevato “disordine”, ovvero una maggiore difficoltà nell’assegnare ciascun record alla propria classe, sulla base degli attributi che caratterizzano la classe.
Si ricorda che il logaritmo in base 2 di un numero x è l’esponente da dare a 2 per ottenere x, cioè se n = log2 x allora 2n = x. Si applica la convenzione 0 log2 0 = 0.
In generale, partendo da una situazione di disordine caratterizzata da entropia H(S), una partizione dei record del training set effettuata rispetto ad un certo attributo A porterebbe ad un nuovo valore di entropia H(S, A), tale per cui H(S, A) = H(S) e quindi ad una diminuzione di entropia.
As esempio prendo il nodo età, ripartisco il data set in due sottoinsieme in funzione dei valori assunti, calcolo l’entropia di questi due sottoinsiemi. Faccio la stessa cosa con l’attributo tipo di autoveicolo. Calcolo la differenza tra l’entropia del data set, e l’entropia generata dai vari attributi. La differenza viene definita guadagno informativo, dove ho maggiore guadagno maggiore informativo vuol dire che l’attributo ha un maggiore valore informativo. Si sceglie quindi quel nodo come nodo radice.
In tale ambito rientra il concetto di GUADAGNO DI INFORMAZIONE (information gain), definito come: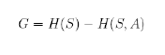
Tale quantità è tanto maggiore quanto più elevata è la diminuzione di entropia ottenuta dopo aver partizionato i dati del training set con l’attributo A.
Il guadagno di informazione ha valori molto elevati in corrispondenza di attributi che sono fortemente informativi e che quindi aiutano a identificare con buona probabilità la classe di appartenenza dei record.
Dunque un criterio di scelta dei nodi di un eventuale albero di classificazione consiste nello scegliere di volta in volta l’attributo A che garantisce una maggiore diminuzione di entropia o che, analogamente, massimizza il guadagno di informazione.
L’algoritmo C4.5 utilizzato (in forma semplificata) negli esempi sviluppati, utilizza le variabili entropia e guadagno di informazione per la scelta dei nodi.
Continua a leggere:
- Successivo: Indice di Gini e indice di misclassificazione
- Precedente: Criteri per la costruzione degli alberi decisionali - controllo della crescita
Per approfondire questo argomento, consulta le Tesi:
- Un analisi statistica su come le recensioni possono influenzare la scelta di acquisto dei consumatori
- Sistemi web-based di analisi strategica: Business Intelligence e Big Data
- Il Data mining a supporto dei processi decisionali in azienda
- L'evoluzione dei sistemi informativi e di controllo aziendali
- Analisi dei processi di CRM nel web: electronic customer relationship management
Puoi scaricare gratuitamente questo appunto in versione integrale.


