Principio di Generalizzazione
Principio di Generalizzazione
Principio di generalizzazione --> si rifà alla teoria degli insiemi, e alla logica classica aristotelica, per cui si formano classi di equivalenza sempre più inclusive. "il sistema inconscio tratta una cosa individuale (persona, oggetto, concetto) come se fosse un membro o elemento di un insieme o classe che contiene altri membri; tratta questa classe come sottoclasse di una classe più generale e questa classe è più generale come sottoclasse o sottoinsieme di una classe ancora più generale e così via". --> Esempio: nel mio inconscio Silvia (al cui interno sono contenuti occhi, bocca, naso eccetera) è parte della classe delle femmine, che fa parte della classe degli esseri umani, che fanno parte della classe più ampia degli esseri viventi e così via, e lo stesso vale per Luca.
L'inconscio non conosce l'individuo Silvia, ma conosce, a diversi livelli di generalizzazione, la funzione proposizionale, che è la caratteristica che accomuna tutti i membri contenuti in una classe (ad esempio la funzione proposizionale "donne" accomuna Silvia, Lucia e tute le donne) --> l'inconscio tende a generalizzare all'infinito.
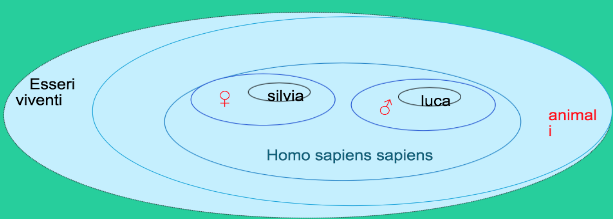
Se sogno Silvia, posso sognarla come rappresentata da qualsiasi altri donna (maggiore livello di generalizzazione), oppure, a un livello di generalizzazione ancora più ampio, può essere rappresentata da qualsiasi altro essere umano. Tra le possibili generalizzazioni l'inconscio ne sceglie alcune: salta da un elemento particolare (Silvia), a classi sempre più ampie, "corre su" per le gerarchie più ampie (esempio: femmine, animali, esseri viventi). L'elemento singolo è sempre trattato come appartenente a classi più ampie, pur conservando però tracce dell'elemento da cui è partito --> dunque nel sogno Silvia può essere rappresentata dalla classe "donne", tuttavia rimane qualche elemento originale di Silvia.
Mentre il principio di generalizzazione rappresenta la logica bivalente (Matte Blanco chiama così la logica tradizionale aristotelica), che si traduce nella costituzione di classi logiche sempre più ampie e potenzialmente infinite, il principio di simmetria è invece apparentemente alieno alla logica, e rappresenta uno scompiglio rispetto alla logica aristotelica.
principio di simmetria: Il sistema inconscio tratta la relazione inversa di qualsiasi relazione come se fosse identica alla relazione stessa, in altre parole tratta le relazioni asimmetriche come se fossero simmetriche.
• Relazione simmetrica: Silvia è la sorella di Alessia --> l'inverso è altrettanto vero, cioè Alessia è la sorella di Silvia
• Relazione asimmetrica: se la Tagini è la prof di Laura, allora la relazione inversa è che Laura è la tesista della Tagini (e non la prof di Laura)
Per il principio di simmetria le relazioni asimmetriche diventano simmetriche, quindi Laura è la prof della Tagini --> 2 cose che non sono uguali vengono trattate come uguali. Questo trattare le relazioni asimmetriche come simmetriche fa sì che scompaiano dei principi logici --> esempio: relazione di tempo --> se domani viene dopo oggi (x viene dopo y), allora oggi non viene dopo domani (y non viene dopo x, ma prima) --> nell'inconscio però questa relazione asimmetrica viene trattata come simmetrica, quindi oggi può venire dopo domani (Y può venire dopo x) --> così scompare la temporalità.
Conseguenze del principio di simmetria: se Silvia fa parte dell'insieme di donne, allora, secondo il principio di asimmetria donne non fa parte dell'insieme di Silvia. Tuttavia l'inconscio opera la simmetria, quindi se Silvia fa parte delle donne, le donne fanno parte di Silvia (oppure: se il mio braccio fa parte del mio corpo, allora il mio corpo fa parte del mio braccio) --> dunque quando si applica il principio di simmetria la parte è necessariamente identica al tutto --> ciò implica che il tutto è incluso in ogni parte in quanto ogni parte è identica al tutto e quindi identica ad ogni altra parte --> ciò è applicabile alle parti di ogni classe: concetti, persone, oggetti materiali, situazioni ecc...
"Quando si applica il principio di simmetria, tutti i membri di un insieme (classe) sono trattati come identici tra loro e identici all'insieme; quindi sono interscambiabili sia rispetto alla funzione proposizionale che definisce la classe (sono interscambiabili ad esempio uomini e donne in quanto appartengono alla funzione proposizionale "esseri umani"), sia riguardo a tutte le funzioni proposizionali che permettono di distinguerli fra di loro ("uomini" e "donne") e attraverso le quali (le funzioni) è possibile affermare in logica aristotelica, che un dato elemento della classe non è identico ad un altro (cioè nella logica aristotelica uomini non sono donne, tuttavia nel principio di simmetria, dato che uomini e donne appartengono entrambi all'insieme "esseri umani", uomini e donne sono identici agli esseri umani e sono identici fra di loro)".
Esempio di logica asimmetrica: Tagini è membro della classe insegnanti e anche Miglioretti: entrambi soddisfano la funzione proposizionale della classe degli insegnanti. Miglioretti soddisfa anche altre proposizioni, dato che è maschio, papà, neurologo. Tagini può soddisfare altre proposizioni, ad esempio femmina, straniera ecc. La loro differenza è descrivibile proprio in termini delle funzioni proposizionali che non hanno in comune --> se Tagini e Miglioretti condividessero tutte le funzioni proposizionali sarebbero a tutti gli effetti indistinguibili (invece ne condividono solo una, e cioè insegnare in Bicocca)--> Miglioretti sarebbe Tagini e Tagini sarebbe Miglioretti. Tuttavia con la logica simmetrica, basta condividere 1 funzione proposizionale per essere identici!
[Secondo il principio di generalizzazione Silvia e Luca non sono identici perché appartengono a due classi diverse.]
Un'altra caratteristica dell'applicazione della simmetria: quando si applica il principio della simmetria, certe classi le cui funzioni proposizionali sono del tipo p e ¬p e perciò sono vuote per definizione, possono invece essere trattate come non vuote. Se p è vivo e ¬p è non vivo (morto), per il principio di contraddizione p e ¬p è impossibile, ma dato che p e ¬p fanno parte di una classe più ampia (tutti i possibili modi di esistere), consegue secondo il principio di simmetria che essere vivo equivale a essere morto --> emerge quindi una nuova classe di quelli che sono vivi e morti --> la classe vivi e morti (p e ¬p), non è più vuota, ma piena.
Finché il principio di generalizzazione opera in ambito discreto (si focalizza su ciò che distingue una classe da tutte le altri classi, o sui singoli elementi contenuti) esprime la logica bivalente. Ma se formiamo classi per mezzo del principio di simmetria, allora ogni elemento della classe si identifica completamente con ogni altro elemento, e con la classe stessa: si viene a creare omogeneità all'interno della classe --> finché opero la generalizzazione posso distinguere tra gli elementi, ma se utilizzo il principio di simmetria si viene a creare una omogeneità tra gli elementi delle classi in cui si è utilizzato il principio di simmetria.
Continua a leggere:
- Successivo: Principio di Simmetria
- Precedente: Matte Blanco
Dettagli appunto:
- Autore: Mariasole Genovesi
- Università: Università degli Studi di Milano - Bicocca
- Facoltà: Psicologia
- Corso: Psicologia
- Esame: Psicologia dinamica
- Docente: Angela Tagini
Altri appunti correlati:
- Il pensiero di Jung
- Psicologia Dinamica
- Psicologia cognitiva ed ergonomia
- Psicologia della disabilità
- Psicologia generale
Per approfondire questo argomento, consulta le Tesi:
- Il soggetto transizionale di G. Benedetti nella terapia non verbale delle psicosi e i suoi collegamenti con il pensiero freudiano
- Psicoanalisi dell'Arte e della Musica
- La religione cattolica e la psicologia clinica: un'analisi della letteratura
- La ribellione dell'erede: il contrasto tra Jung e Freud
- Molteplici personalità e alter ego: David Bowie, l’uomo che sfuggì alla follia
Puoi scaricare gratuitamente questo appunto in versione integrale.